[방송통신대학교]데이터정보처리입문 1학기 중간평가 출석수업대체과제물

1-1. 1990년부터 2019년까지의 연도별 전국 총출생성비를 시계열도표로 나타내고 전체적인 경향을 
설명하시오.
출생성비는 여아 100명당 남아 수를 말하며, 1991년, 1997년에 눈에 띄게 출생성비가 감소한 것을 
볼 수 있었고, 1998년도에 출생성비가 증가 햇으나 전체적으로 출생성비가 서서히 감소하고 있는 
추세이며, 광주광역시가 가장 출생성비가 감소하였다.
1-2. 1990년부터 2019년까지의 연도별 서울과 부산의 총출생성비를 하나의 시계열도표에 나타내고 
비교하여 설명하시오.

부산의 출생성비는 지속적으로 감소 하고 있으며 서울의 출생성비도 지속적으로 감소하고 있는
추세를 확인 할 수 있었다.

1-3. 1993년부터 2019년까지의 연도별 전국 합계출산율을 시계열도표로 나타내고 전체적인 경향을 
설명하시오.

합계출산율은 여성 1명이 평생동안 낳을 것으로 예상되는 평균 출생아수를 나타낸 지표로서 출산력 
수준을 나타내는 국제적 지표을 말한다.
최근 혼인 감소 등 출산에 미치는 요인들의 변화에 따라, 2001년에 이어 2002년에 크게 감소한 
이후 1.3을 넘지 못하는 낮은 합계출산율을 보이고 있다.

2-1. 평균, 중앙값, 표본분산, 표본표준편차, 변동계수를 구하여 분포의 특징을 설명하시오.
평균 : 47.44615
중앙값 : 48
표본분산 : 404.3135
표본표준편차 : 20.10755
변동계수 : 0.4237972

분포는 좌우 대칭의 형태를 띠며, 평균치에서 확률값이 가장 높다.

2-2. 줄기-잎 그림, 히스토그램, 상자그림을 그리고 분포의 특징을 설명하시오.

<줄기-잎 그림>

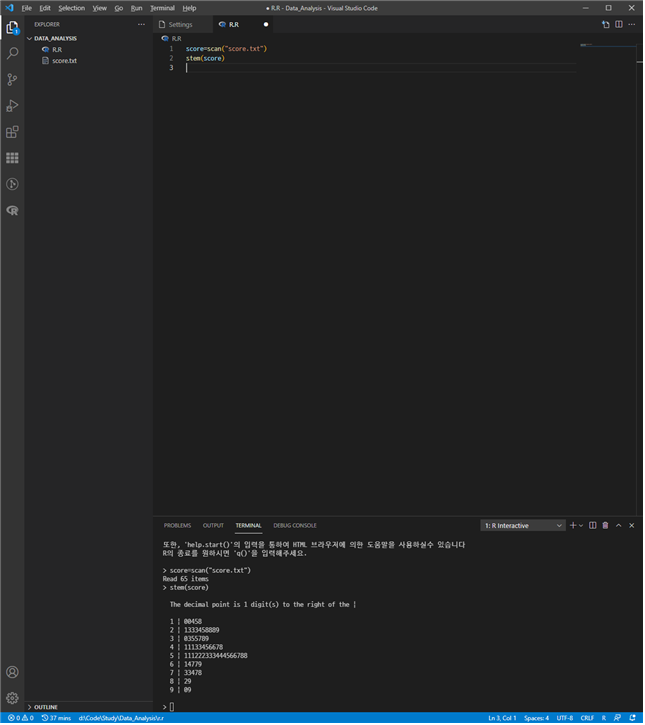
구분기호 왼쪽은 십의자리를 나타냅니다. 
자료의 분포를 파악하기가 용이하다. 
원데이터의 파악이 가능하다.(중앙값)

<히스토그램>

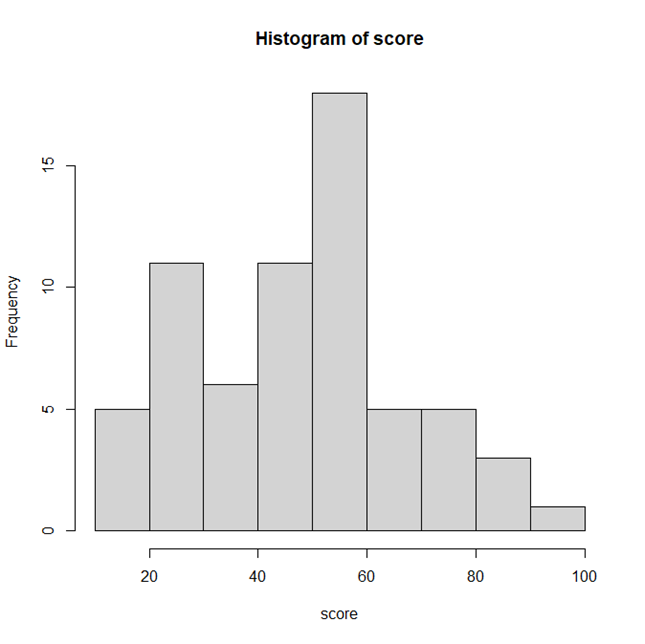
일변량 데이터를 계급으로 나누어 각 도수를 구한 후 x축은 계급, y축은 도수를 막대의 형태로 
나타낸 그림이다.

<상자그림>

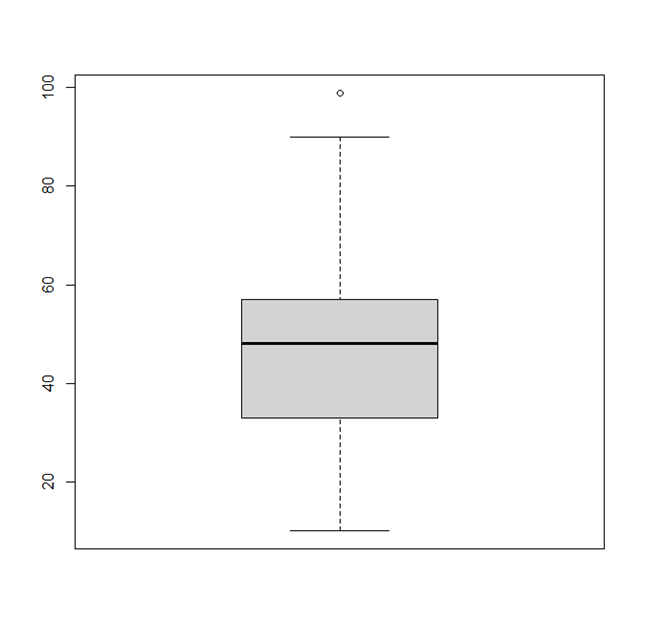
중앙값, 제 1사분위수, 제 3사분위수, 최댓값 , 최솟값을 다섯 숫자 요약(5 number summary)라고 
한다. 이를 그림으로 나타낸 것이 상자그림이다.

3. 교재4장 연습문제 1번
<독립성 검정 방법에 대하여>
관측된 자료들이 어떤 특성을 갖는지에 따라 몇 개의 범주(category)로 나뉘어 분류 정리되었을 때, 각 범주에 속하는 도수(frequency)로 이루어진 자료 변수를 범주형 변수라고 하며, 다음과 같은 형태의 표를 이차원 분할표라고 한다.

<2차원 분할표>

		변 수 B
		값 B1	값 B2	값 B3	값 B4	합 계
변 수 A	값 A1	∱11	∱12	∱13	∱14	∱1∙
	값 A2	∱21	∱22	∱23	∱24	∱2∙
	값 A3	⋯	⋯	⋯	⋯	∱3∙
	값 A4	⋯	⋯	⋯	⋯	∱4∙
	값 A5	∱51	∱52	∱53	∱54	∱5∙
	합 계	∱∙1	∱∙2	∱∙3	∱∙4

독립성 검정에서의 귀무가설은

: 행과 열 변수는 서로 독립이다.

로서, 총 표본의 크기는 만이 미리 결정되어 있다면 번째 반응을 나타내는 개체의 총수는

 

이 된다. 두 변수 A와 B가 서로 독립이라면
로서, 귀무가설하에서의 각 칸의 기대도수는

이며 검정통계량은 다음과 같다.